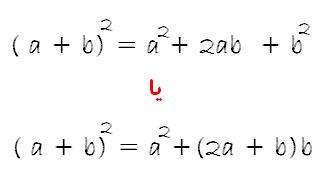موضوع: آموزش
در این مقاله سعی شده است تا به بررسی جذر اعداد به روشی که در پایه سوم راهنمایی گفته شده بپردازیم و برای ان دلیل و برهانی بیابیم.
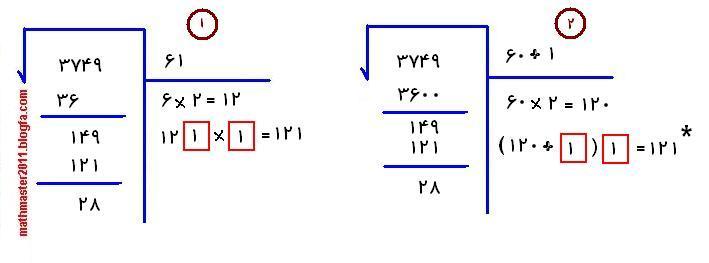
در تصویر زیر به دو صورت حاصل جذر 3749 را بدست آورده ایم.
در تصویر 1 با روشی که در کتاب سوم راهنمایی گفته شده حاصل جذر 3749 را بدست اورده ایم. ولی در تصویر 2 قصد داریم در این روش تغیراتی ایجاد کنیم. اگر از سمت راست عدد 3749 را دو رقم ، دو رقم جدا کنیم متوجه می شویم که حاصل جذر عددی دو رقمی خواهد بود که اولین عدد آن رقم 6 خواهد بود که چون در مرتبه دهگان قرار دارد. به جای نوشتن عدد 6 ، عدد 60 را می نویسیم. مجذور 60 یعنی 3600 را زیر عدد 3749 می نویسیم و از هم کم می کنیم. سپس مانند تصویر 1 عدد 60 را دو برابر می کنیم. ولی به قسمت * تصویر 2 توجه کنید. این قسمت هیچ تفاوتی با روشی که کتاب اشاره کرده نمی کند. فقط به جای 121 نوشته شده 1+120 .
حال ببینیم با عدد 3749 چه کردیم؟
همان طور که مشاهده کردید در این روش جذر گرفتن از بسط دو جمله ای زیر استفاده شده است.
حال می خواهیم با استفاده از این بسط ریشه دوم عدد 50000 را با تقریب کمتر از یک بدست آوریم.
با استفاده از این فرایند قادر خواهیم بود ریشه سوم ، چهارم و ... را نیز محاسبه کنیم.
ولی هنوز این سوال باقی است که چرا در امتحان جذر باید دو برابر جذر به اضافه یک از باقیمانده ی جذر بزرگتر باشد؟
چون می خواهیم جواب تا یک رقم اعشار بدست آید باید (1×3) سه رقم اعشار داشته باشیم و برای رشه سوم سه رقم سه رقم جدا می کنیم.
پس جواب ما دورقمی و دارای یک رقم اعشار خواهد بود "دهم/یکان ، دهگان"
ریشه سوم 187 بیش تر از 5 و کم تر از 6 است. البته 5 در ارزش مکانی دهگان خواهد نشست پس:

حال با توجه به a3+(3a2+3ab+b2)b مقادیر 3a2 و 3a را محاسبه می کنیم .۵۰=a
و سعی داریم: مقدار b را در 3a2+3ab+b2)b) با ارزش مکانی یکان پیدا کنیم لذا:
در این مرحله حدس زدن عدد بعدی راحت به نظر نمی رسد و باید گزینه هایی را امتحان کرد.
ابتدا عدد 5 را قرار می دهیم داریم:
41375=5(52+5×150+7500)
که 41375 از 62643 کم تر است پس با 8 امتحان می کنیم
70112=8(82+8×150+7500)
و این جواب از 62643 بیشتر است در نتیجه 8 مناسب نیست و عدد 7 را قرار می دهیم.
60193=7(72+7×150+7500)
و 60193 از 62643 کم تر است لذا 7 عدد صحیح است.
بنابراین:

برای پیشروی در محاسبه بار دیگر مقادیر 3a2 و 3a را محاسبه می کنیم
البته تا اینجا جواب 57 را بدست آورده ایم پس a را 57 در نظر می گیریم.

و بایستی عدد جدید را با ارزش مکانی دهم حدس بزنیم

بنابراین ریشه سوم 187643 تا یک روش اعشار 2/57 می باشد و باقیمانده نیز 752/493 می باشد.
a+b)3 = a3+3a2b+3ab2+b3 = a3+(3a2+3ab+b2)b)
a+b)4 = a4+4a3b+6a2b2+3ab3+b4 = a4+(4a3+6a2b+3ab2+b3)b)
و . . .
مثال:ریشه سوم عدد 187643 را تا یک رقم اعشار بدست می آوریم.
رابطه مد نظر ما: a3+(3a2+3ab+b2)b
مناسب است به این نکته نیز اشاره کنم که:اگر جذر عددی مانند A را a محاسبه کرده باشیم. " اگر a عددی اعشاری باشد از ممیز آن برای این بخش از امتحان جذر صرف نظر می شود" در این صورت باقیمانده این جذر باید کم تر از 2a+1 باشد زیرا: a+1)2=a2+2a+1 ) بنابراین:
a+1)2-a2=2a+1)
و یا: در محاسبه ریشه سوم باقیمانده باید از باقیمانده a+1)3-a3 ) کم تر باشد
پس در محاسبه ریشه سوم باقیمانده : باید از مجموع (سه برابر مربع جواب بدست آمده با سه برابر جواب بدست آمده و عدد یک ) کم تر باشد
امتحان جذر
فرض می کنیم جذر عدد a برابر b و باقیمانده ی جذر r باشد در این صورت داریم:
a< (b+1)2
(*) a<b2+2b+1
با توجه به اینکه توان دوم جذر به اضافه باقیمانده برابر a است پس: a=b2+r
در رابطه ی (*)به جای a مساوی آن یعنی a=b2+r
را قرار می دهیم پس:
b2+r<b2+2b+1
r<2b+1
یعنی: 2 برابر جذر به اضافه یک بزرگتر از باقیمانده جذراست.